剑指 Offer 04. 二维数组中的查找

难度 中等

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

1
2
3
4
5
6
7
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

限制：

1
2
0 <= n <= 1000
0 <= m <= 1000

思路

若使用暴力法遍历矩阵 matrix ，则时间复杂度为 O(NM)O(NM) 。暴力法未利用矩阵 “从上到下递增、从左到右递增” 的特点，显然不是最优解法。

刚开始的想法是行内做二分，列内也做二分，每次排除四分之三的数据，然后发现等矩阵小了之后好像就不方便找了，写起来很麻烦，然后参考了下题解，想到了这是个二叉搜索树就用二叉搜索树的性质了

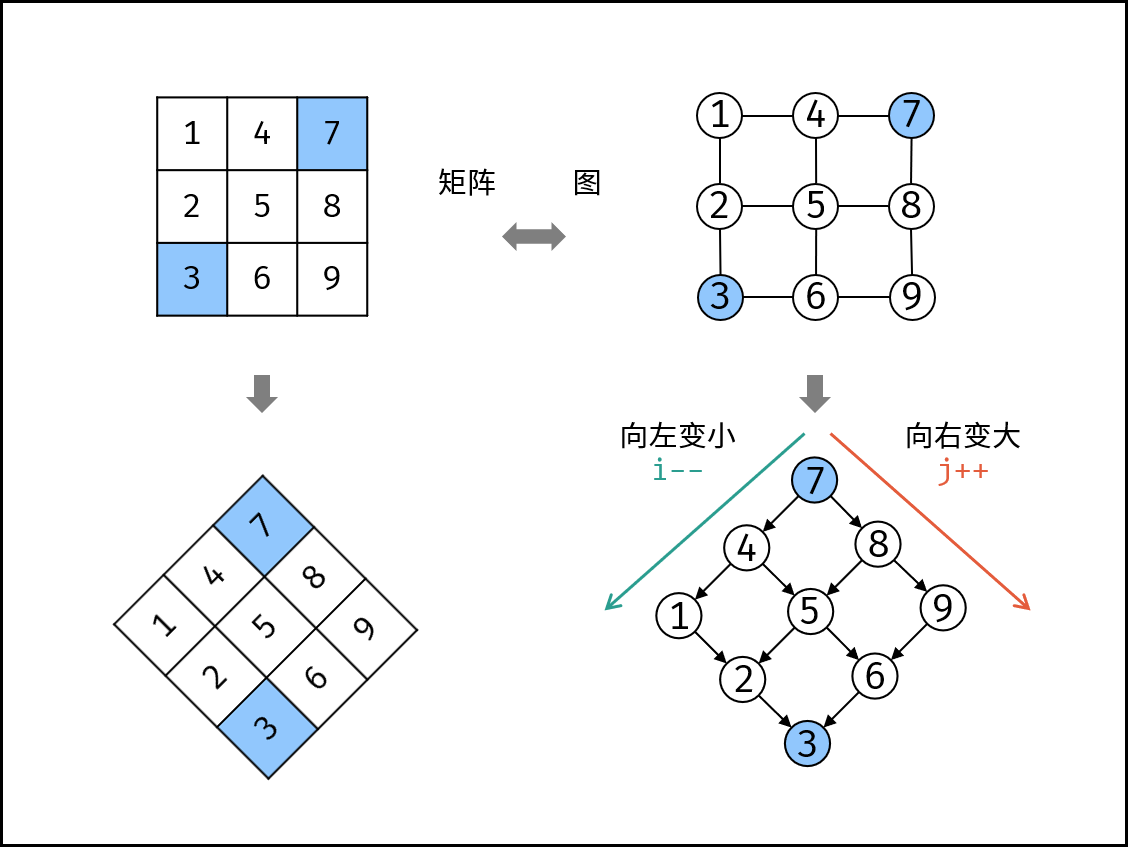
如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

Picture1.png

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        int i,j;
        i = matrix.size()-1;  j=0;
        while( i>=0 && j < matrix[0].size())
        {
            if(matrix[i][j] > target) i--;
            else if(matrix[i][j] < target) j++;
            else if(matrix[i][j] == target) return true;
        }
        return false;
    }
};