剑指 Offer 11. 旋转数组的最小数字

难度 简单

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

示例 1：

1
2
输入：[3,4,5,1,2]
输出：1

示例 2：

1
2
输入：[2,2,2,0,1]
输出：0

注意：本题与主站 154 题相同：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/

思路

解题思路：
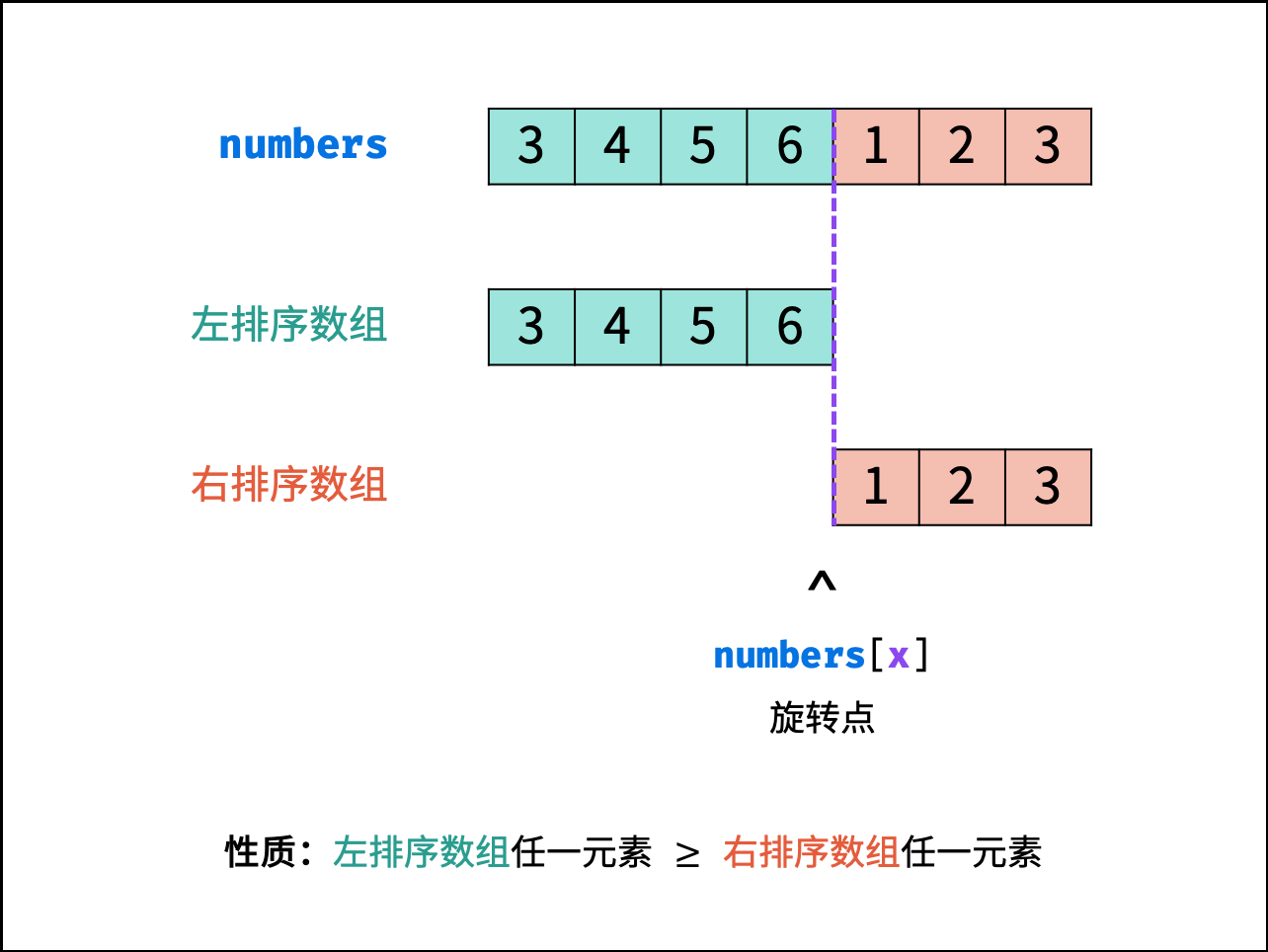
为精简篇幅，本文将数组 numbers 缩写为 nums。

如下图所示，寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 nums[x] ，称 x 为 旋转点 。

Picture1.png

排序数组的查找问题首先考虑使用 二分法 解决，其可将 遍历法 的 线性级别 时间复杂度降低至 对数级别 。

算法流程：

  1. 初始化： 声明 i, j 双指针分别指向 nums 数组左右两端；
  2. 循环二分： 设 m = (i + j) / 2为每次二分的中点（ “/“ 代表向下取整除法，因此恒有 $i \leq m < j$ ），可分为以下三种情况：
    1. 当 nums[m] > nums[j] 时： m 一定在 左排序数组 中，即旋转点 x 一定在 [m + 1, j] 闭区间内，因此执行 i = m + 1;
      1. 当 nums[m] < nums[j]时： m 一定在 右排序数组 中，即旋转点 x 一定在[i, m] 闭区间内，因此执行 j = m；
      2. 当 nums[m] = nums[j]时： 无法判断 m 在哪个排序数组中，即无法判断旋转点 x 在 [i, m] 还是 [m + 1, j] 区间中。解决方案： 执行 j — 缩小判断范围，分析见下文。
  3. 返回值： 当 i = j时跳出二分循环，并返回 旋转点的值 nums[i] 即可。

正确性证明：
当 nums[m] = nums[j]] 时，无法判定 m 在左（右）排序数组，自然也无法通过二分法安全地缩小区间，因为其会导致旋转点 x 不在区间 [i, j] 内。举例如下：

设以下两个旋转点值为 00 的示例数组，则当 i = 0,j=4 时 m = 2 ，两示例结果不同。
示例一 [1, 0, 1, 1, 1]：旋转点 x = 1，因此 m = 2在 右排序数组 中。
示例二 [1, 1, 1, 0, 1]：旋转点 x = 3 ，因此 m= 2 在 左排序数组 中。

而证明 j = j - 1 正确（缩小区间安全性），需分为两种情况：

  1. 当 x < j 时： 易得执行 j = j - 1 后，旋转点 xx 仍在区间 [i, j]内。

  2. 当 x = j 时： 执行 j = j - 1后越过（丢失）了旋转点 x ，但最终返回的元素值 nums[i] 仍等于旋转点值 nums[x] 。

    1. 由于 x = j ，因此 $nums[x] = nums[j] = nums[m] \leq number[i]$;
    2. 又由于 $i \leq m <j$恒成立，因此有 m < x ，即此时 m 一定在左排序数组中，因此 $nums[m] \geq nums[i]$ ;
      综合 1. , 2. ，可推出 nums[i] = nums[m]nums[i]=nums[m] ，且区间 [i, m][i,m] 内所有元素值相等，即有：
  • 此时，执行 j = j - 1 后虽然丢失了旋转点 xx ，但之后区间 [i, j] 只包含左排序数组，二分下去返回的一定是本轮的 nums[i]，而其与 nums[x] 相等。
  • 综上所述，此方法可以保证返回值 nums[i] 等于旋转点值 nums[x] ，但在少数特例下 $i \ne x$ ；而本题目只要求返回 “旋转点的值” ，因此本方法正确。

补充思考： 为什么本题二分法不用 nums[m] 和 nums[i] 作比较？

二分目的是判断 m 在哪个排序数组中，从而缩小区间。而在 nums[m] > nums[i]情况下，无法判断 mm 在哪个排序数组中。本质上是由于 j 初始值肯定在右排序数组中； i 初始值无法确定在哪个排序数组中。举例如下：

对于以下两示例，当 i = 0, j = 4, m = 2 时，有 nums[m] > nums[i] ，而结果不同。
[1, 2, 3, 4 ,5]旋转点 x = 0 ： m 在右排序数组（此示例只有右排序数组）；
[3, 4, 5, 1 ,2]旋转点 x = 3 ： m 在左排序数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int minArray(vector<int>& numbers) {
        int Left,Right,mid;
        Left = 0; Right = numbers.size()-1;
        while(Left < Right)
        {
            mid = (Left+Right)/2;
            if(numbers[mid] > numbers[Right]) Left = mid+1;
            else if(numbers[mid] < numbers[Right]) Right = mid;
            else if(numbers[mid] == numbers[Right]) Right--;
        }
        return numbers[Left];
    }
};